电子圆二色谱(ECD)计算结果分析之科顿效应的解释与归属
总结一下ECD计算的流程:1)CONFLEX进行构象分析,获得低能构象集;2)Gaussian 09对每个构象进行能量优化(关键词:opt apfd/6-311+g(2d,p) scrf=(iefpcm,solvent=methanol);3)对每个用DFT优化后的构象进一步计算ecd(关键词:td=(nstates=30) apfd/6-311+g(2d,p) scrf=(iefpcm,solvent=methanol) );4)玻尔兹曼加权的图谱制作、与实验值进行比较。
完成电子圆二色谱(ECD)的计算后,需要将不同构型的玻尔兹曼平均ECD图谱与实验ECD图谱进行对比,选取最接近实验图谱的,从而确定化合物的立体构型。在此之后,通常需要对ECD的科顿效应(Cotton Effect)进行分子轨道层面的解释。
玻尔兹曼平均ECD图谱是多个构象的ECD图谱的综合结果,但在解释科顿效应时,只能以单个构象来解释。因此,我们选取对平均ECD图谱贡献最大的即能量最低的一个(或多个)构象。下面以 “第一届量化计算与药物设计实用技术培训班”上的ECD计算结果为例,讲述如何计算玻尔兹曼权重因子、绘制分子轨道图以及解释ECD的科顿效应。
一、计算玻尔兹曼权重因子
通过SpecDis将各个构象的能量及光谱抽取出来后,得到两个文件夹heat和spectra,将heat中的文件全部复制到spectra文件夹中,然后使用SpecDis进行玻尔兹曼平均:
-
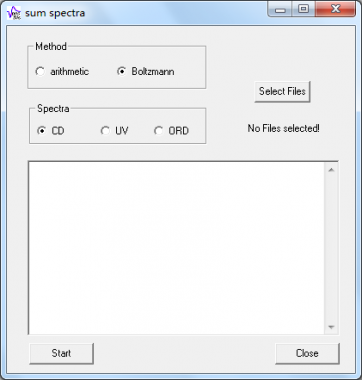
Tools > sum spectra
-
Method选择Boltzmann,Spectra选择CD,点击Select Files按钮。
-
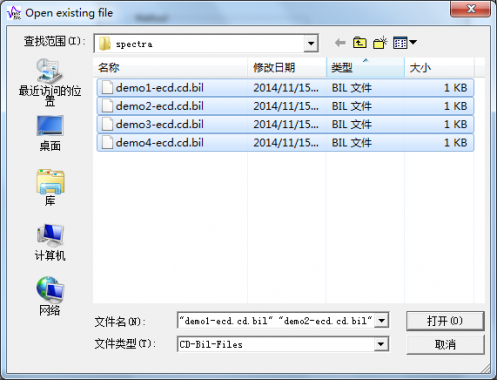
文件类型选择CD-Bil-Files,选择spectra文件夹中扩展名为.cd.bil的所有文件,点击打开。
-
点击Start。
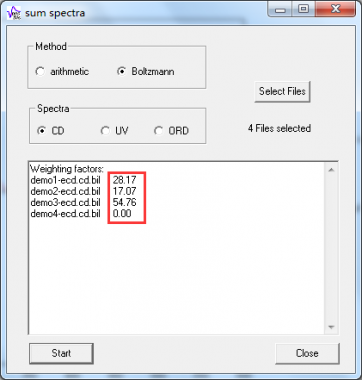
各构象的玻尔兹曼权重因子(即构象分布比例)在输出文本框中列出,如demo1的权重因子是28.17,即该构象占比28.17%:
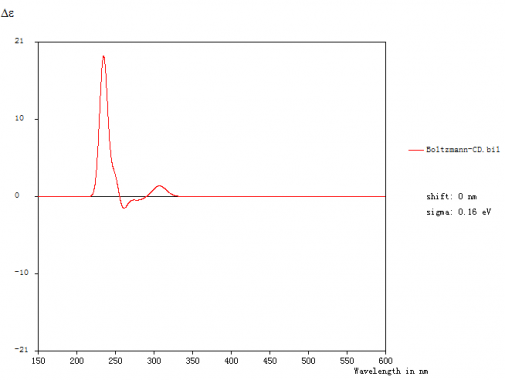
同时,主界面中会显示玻尔兹曼平均ECD曲线:
二、绘制分子轨道图
由第1步的结果,优先考虑权重因子最大的构象demo3进行分析。
1、查看激发态信息
-
用文本方式(如Notepad++)打开ECD计算结果文件(demo3-ecd.log)。
-
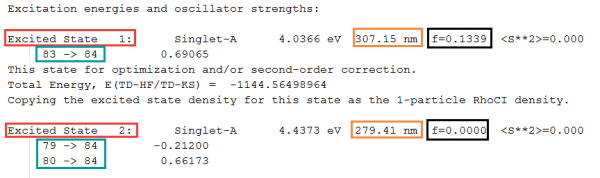
查找含有Excitation energies and oscillator strengths的一行。
该行下面是每一个激发态的信息:
图中,红框部分是激发态序数,蓝框部分是电子跃迁的分子轨道及跃迁方向,橙框部分是吸收波长,黑框部分是振子强度。
2、绘制第一激发态的分子轨道图
从上图中找到第一激发态对应的分子轨道是83和84。
-
将demo3-ecd.log拖至GaussView 5。
-
Edit > MOs
打开MOs窗口。窗口上方右侧列出各个分子轨道对应的序号及能量,其中,有红色箭头(表示自旋相反的电子)的是占据轨道,无红色箭头的是未占轨道。默认情况下,最高占据轨道(HOMO)与最低未占轨道(LUMO)会被选择并标黄色。在这个例子中,83是HOMO,84是LUMO。
-
点击New MOs视图,Method选择Generate New Chk File,Model保持默认,
-
Basis Set设置为实际计算采用的基组,这里设置为6-31G,d,点击Generate按钮。
调用Gaussian 09进行计算,完成后,Visualize视图由灰变亮。
-
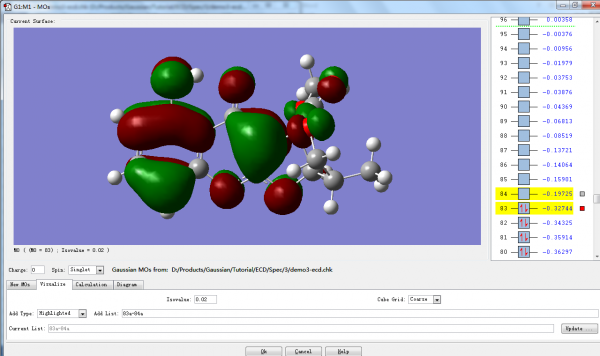
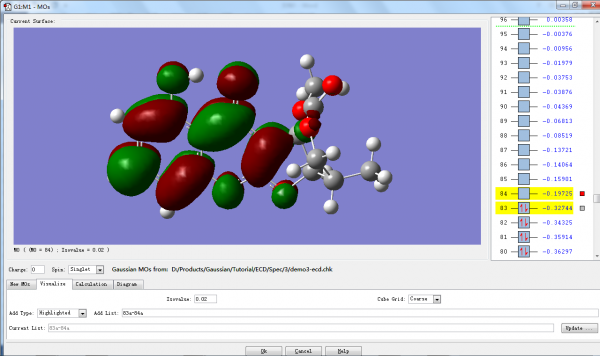
点击Visualize视图,采用默认参数,点击Update …
片刻后,视图右侧标红色方框的分子轨道将显示在视图左侧。
3、对于其他激发态,可以找到相应的一对(或多对)分子轨道,然后以同样方式绘制分子轨道图。
三、解释科顿效应
由上图可知,玻尔兹曼平均ECD图谱中307.15 nm附近的吸收峰(正的科顿效应)是由于电子从分子轨道83跃迁到84引起的,即π->π*。